武汉大学《计算机组成与设计》课程的课程笔记,使用 David Patterson 的教材书,并针对书中的一些不清晰的地方做了详尽的注解。
The notes of the course Computer Composition and Design in Wuhan University. Use the textbook of David Patterson, and make detailed annotations for some unclear points in the book.
Operations on integers:
- Addition and subtraction
- Multiplication and division
- Dealing with overflow
Floating-point real numbers:
- Representation and operations
Unsigned Binary Integers and 2s-complement Signed Integers
Given an n-bit number:
Range: $0$ to + $2^{n}-1$.
- Using 64 bits: 0 to +18,446,774,073,709,551,615.
Given an n-bit number:
Range: $-2^{n – 1}$ to + $2^{n – 1}-1$.
- Bit 63 is sign bit: 1 for negative numbers, and 0 for non-negative numbers.
- Complement means 1 → 0, 0 → 1, then we know that:
- Sign Extension: Representing a number using more bits and preserve the numeric value. Usually replicate the sign bit to the left: 0000 0010 → 0000 0000 0000 0010
- In RISC-V instruction set:
lb: sign-extend loaded byte;lbu: zero-extend loaded byte.
Hexadecimal: Base 16. Compact representation of bit strings, 4 bits per hex digit.
- Example:
0xECA86420→ 1110 1100 1010 1000 0110 0100 0010 0000
Integer Addition

硬件规模总是有一定限制的,比如字宽为 64 位,当运算结果超过这个限制时,就会发生溢出。
- 在加法中,当不同符号的操作数相加时,不会发生溢出,因为总和一定不会大于其中任意一个操作数。由于操作数可以表示成 64 位且其总和不大于任一操作数,所以总和也一定能表示成 64 位。
- 类似地,当相同符号的操作数相减时,也不会发生溢出。
- 缺少第 65 位意味着当溢出发生时,符号位被结果的值占用而非结果的正确符号。由于溢出结果只可能多一位,所以只有符号位可能是错误的。因此,当两个正数相加但和为负数时,说明发生了溢出,反之亦然。这个假的和值意味着产生了向符号位的进位。
- 无符号整数通常用于表示忽略溢出的内存地址。编译器可以轻松检查出使用分支指令的无符号溢出。如果总和小于两数任何之一,则加法溢出,如果差大于被减数,则减法溢出。
无论数的表示形式如何,计算机的有限字长意味着算术运算可能会产生过量而无法用这种固定字长表示的运算结果,即发生溢出。虽然无符号数的溢出容易检测,但无符号数通常使用自然数做地址运算,而程序通常不需要检测地址计算的溢出,所以这些溢出总被忽略。二进制补码对检测溢出提出了更大的挑战,但仍有一些软件系统需要识别溢出,因此今天所有的计算机都支持溢出检测。
在通用微处理器中不常见的一个特性是饱和操作。饱和 (saturation) 意味着当计算溢出时,结果设置为最大正数或最小负数,而不是像二进制补码运算那样采用取模计算。饱和操作可能更适用于多媒体操作。
Float Addition
Float in RISC-V
Floating Point: Representation for non-integral numbers, including very small and very large numbers.
- Like scientific notation: $\pm 1.xxxxxx_{2} \times 2^{yyyyy}$. 该计数法在小数点左边只有一个数字。科学计数法中整数部分没有前导 0 的数字称为规格化数。由于基数不是 10,这个小数点被成为二进制小数点。支持这种数的计算机运算称为浮点运算,称作 “浮点” 是因为它表示二进制小数点不固定的数字,这与整数表示法不太相同。C 语言中使用 float 来表示这些数字。
- Types
floatanddoublein C.floatis single precision (32-bit) anddoubleis 64-bit. - 优点:简化了包含浮点数的数据交换;简化了浮点运算算法;提高了可储存在字中的数据的精度。
浮点表示的设计者必须在尾数的位数大小和指数的位数大小之间找到一个平衡,因为固定的字大小意味着若一部分增加一位,则另一部分就得减少一位,即要做精度和范围之间的权衡:增加尾数位数的大小可以提高小数精度,增加指数位数的大小可以增加数的表示范围。Good design demands good compromise.
下面是 RISC-V 浮点数的表示方法:

浮点数可以表示为:$(-1)^{\text{S}} \times \text{F} \times 2^\text{E}$,其中 F 是尾数字段表示的值,E 是指数字段表示的值。
- 范围:$\ 2.0_{10} \times 10^{\pm38}$ 。
- 浮点运算中也会发生溢出中断,即因指数太大无法在指数字段中表示出来(上溢),或非零小数是否变得小到无法表示(下溢)。
于是,在 C 语言中引入双精度,需要一个 RISC-V 双字才能表示。指数为 11 位,尾数为 52 位。

- 范围:$\ 2.0_{10} \times 10^{\pm308}$ 。
在上溢或下溢时,有些计算机会通过引发例外(有时也称作中断)来告知问题的出现。例外或中断在本质上是一种非预期的过程调用。造成溢出的指令的地址保存在寄存器中,并且计算机会跳转到预定义的地址以调用相应的例外处理程序。中断的地址被保存下来。以便在某些情况下可以在执行纠正代码之后继续执行原程序。 RISC-V 计算机不会在上溢或下溢时引发例外,但软件可以读取浮点控制和状态寄存器(fcsr)来检测是否发生上溢或下溢。
IEEE 754 Float Standard
This standard was developed in response to divergence of representations and portability issues for scientific code. Now it is almost universally adopted.
为了将更多的位打包到数中,IEEE 754 让规格化二进制数的前导位 1 是隐含的。因此,在单精度下,该数实际上是 24 位长(隐含 1 和 23 位尾数),在双精度下则为 53 位长。为了更精确,我们使用术语有效位数来表示隐含的 1 加上尾数,当尾数是 23 或 52 位数时,有效位数是 24 或 53 位。由于 0 没有前导 1,因此它被赋予保留的阶码 0,以便硬件不会给它附加一个前导位 1。
因此 $00 \ldots 00_2$ 代表 0,其他的数就是用前面的形式,加上隐含的 1:
其中,尾数位表示大小在 0 到 1 之间的小数,$\mathrm{E}$ 表示指数字段的值。
如果将尾数的各位从左到右依次用 $\mathrm{s} 1, \mathrm{~s} 2, \mathrm{~s} 3, \cdots$ 来表示的话,则数的值为:
- IEEE 754 的其他特征是用特殊符号来表示异常事件。例如,软件可以将结果设置为代表正负无穷的位模式,而不是除零中断。当程序员打印结果时,程序将输出一个无穷大的符号。
- 符号 NaN 的目的是让程序员可以推迟程序中的一些测试和决定,等到方便时候再进行。
- 符号位位于最高位可以快速判断数的正负,便于排序。
- 把指数放在尾数前也便于排序,因为只要两个数的指数部分符号相同,那么具有更大指数的数就一定更大。
- 为了防止负指数对简化排序的挑战,IEEE 754 将最小负值数表示为 $00…00_{2}$,并将最大的正指数表示为 $11…11_{2}$,这种表示法被称为移码表示法。IEEE 规定单精度的偏移值为 127,因此指数为 -1 表示为 126。双精度的指数偏移值为 1023。
- 单精度浮点数的表示精度为十进制小数后 6 位,双精度为后 16 位。


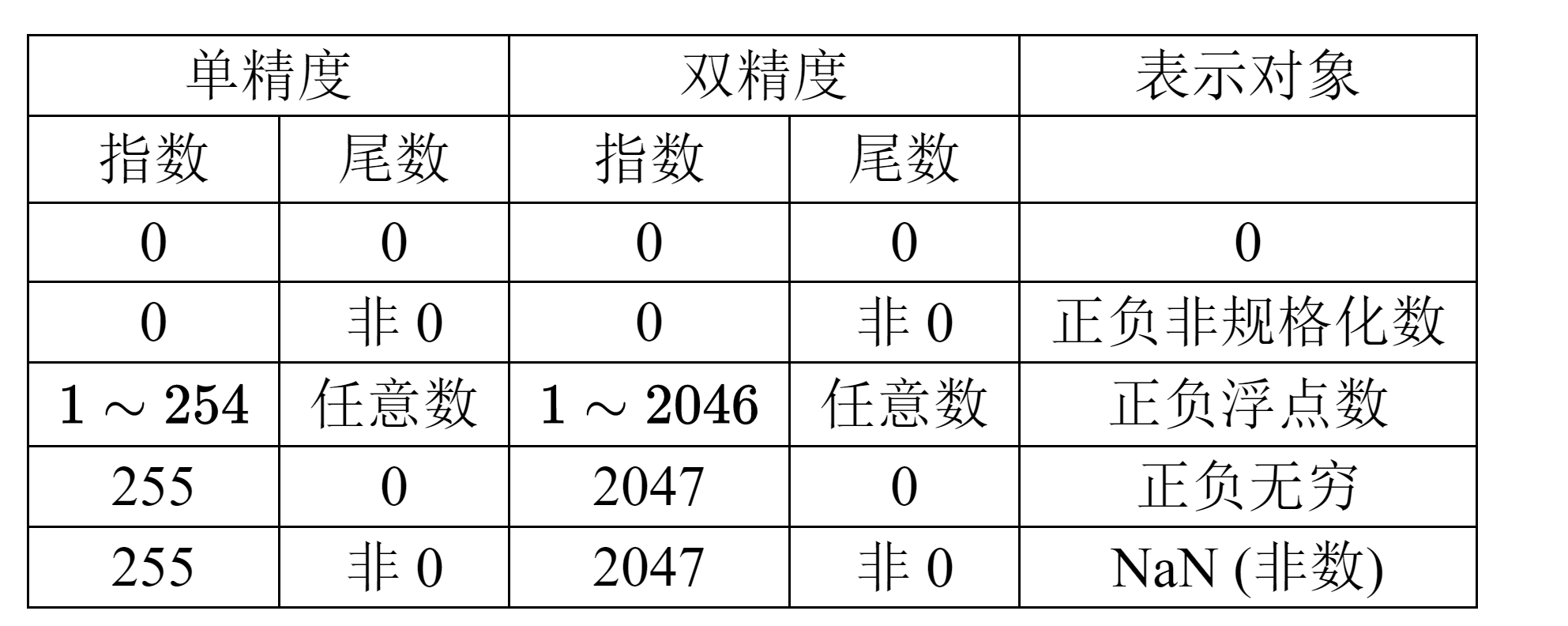
Floating-Point Addition
Decimal Procedure:
- Align decimal points; 将指数较小的数的有效数位右移,直到其指数与较大的数相同;
- Add significands;
- Normalize result & check for over/underflow;
- Round and renormalize if necessary. (4 bit)
Binary Example:
- $1.000_{2} ×2^{–1} + –1.110_{2} ×2^{–2}$
- Align binary points: $1.000_{2} ×2^{–1} + –0.111_{2} ×2^{–1}$
- Add significands: $0.001_{2} ×2^{–1}$
- Normalize result & check for over/underflow: $1.000_{2} ×2^{–4}$
- Round: 0.0625